In this project I implement AB test in numpy. I compare the result with scipy's ttest results. This is an exercise in hypothesis testing and we will still be using scipy t & chi squared distribution class to get the t and chi squared cumulative distribution function. The t tests can be one or two sided depending on the parameter input.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
from scipy import stats
from scipy.stats import chi2, chi2_contingency
from t_test import p_value, welch_p_value, chi2_p_valueThe functions can be found in t_test.py file in the repo. We load a fake advertisement click data to test the efficacy of the tests. Action A=1 implies Ad A was clicked vs Ad B. The idea is to test if Ad B was better than Ad A for the click action.
# get data
df = pd.read_csv('advertisement_clicks.csv')df.head().dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| advertisement_id | action | |
|---|---|---|
| 0 | B | 1 |
| 1 | B | 1 |
| 2 | A | 0 |
| 3 | B | 0 |
| 4 | A | 1 |
a = df[df['advertisement_id'] == 'A']
b = df[df['advertisement_id'] == 'B']
a = a['action']
b = b['action']Lets observe the distribution of the data using sns dist plot.
fig, ax = plt.subplots()
sns.distplot(a, ax=ax)
sns.distplot(b, ax=ax)print("a.mean:", a.mean())
print("b.mean:", b.mean())a.mean: 0.304
b.mean: 0.372
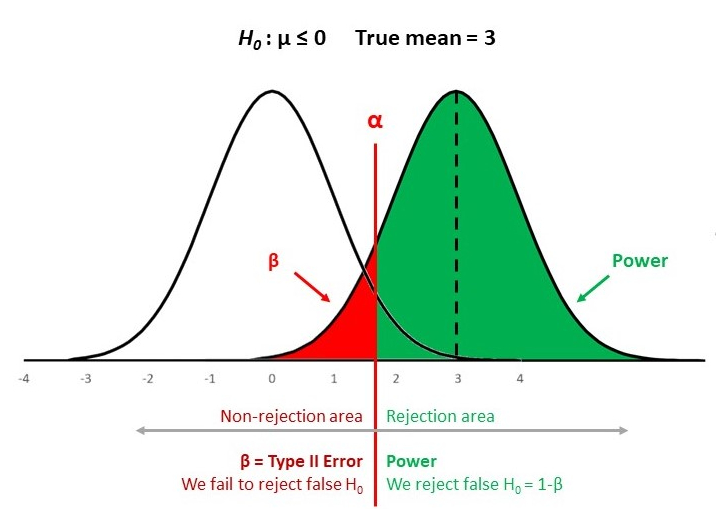
The means of the two distibutions can be seen above. Now, we perform the t-test and compute the p value and the score below and compare it with the stats internal implementation. The Null hypothesis is that 2 independent samples (click actions for a & b) have identical average (expected) values. This is a two-sided test.
t,p = p_value(b,a,True)t: 3.221173213801983 p: 0.0012971905467125122
t, p = stats.ttest_ind(b,a)
print("t:\t", t, "p:\t", p)t: 3.2211732138019786 p: 0.0012971905467125246
Here we observe a p-value < 0.05 , with positive t statistic. Hence we reject the null hypothesis. Since we did two sided test, we can safely say that Ad B performed significantly different than Ad A i.e. performed significantly better than Ad A and not significantly worse than Ad A. Finally, we note that both the implementations (ours vs scipy.stats) have given identical results. The t-test above assumed that the sample means of two Ads being compared were normally distributed with equal variance. Welch's t-test is designed for unequal sample distribution variance, but the assumption of sample distribution normality is still maintained. The Welch p value and the score are computed and compared stats internal implementation.
t,p = welch_p_value(b, a, True)Welch t-test
t: 3.221173213801983 p: 0.001297241037400143
t,p = stats.ttest_ind(a, b, equal_var=False)
print("t:\t", t, "p:\t", p)t: -3.2211732138019786 p: 0.0012972410374001632
One of the assumption of the t-test was independence of the test distributions. We can check for independence using the Chi squared test. Here, we compute the Pearson chi squared statistic and compare with stats internal implementation.
chi2_p_value(b,a, dof=1)Chi2 test
p: 0.0013069502732125926
0.0013069502732125926
A_pos = a.sum()
A_neg = a.size - a.sum()
B_pos = b.sum()
B_neg = b.size - b.sum()
contingency_table = np.array([[A_pos, A_neg], [B_pos, B_neg]])
chi2, p,_, _ = stats.chi2_contingency(contingency_table,correction=False)
print("p:\t", p)p: 0.0013069502732125406
Finally, we perform a one-sided ttest for non categorical distribution. We load a fake distribution of convergence rates for 2 websites. The null Hypothesis is that both website have same convergence.
data= pd.read_csv("conversion.csv")data.head().dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Day | Conversion_A | Conversion_B | |
|---|---|---|---|
| 0 | 1 | 0.15 | 0.19 |
| 1 | 2 | 0.12 | 0.20 |
| 2 | 3 | 0.18 | 0.18 |
| 3 | 4 | 0.19 | 0.22 |
| 4 | 5 | 0.17 | 0.19 |
print("a.mean:", data["Conversion_A"].mean())
print("b.mean:", data["Conversion_B"].mean())a.mean: 0.16200000000000003
b.mean: 0.19333333333333338
fig, ax = plt.subplots()
sns.distplot(data["Conversion_A"],ax=ax)
sns.distplot(data["Conversion_B"], ax=ax)<matplotlib.axes._subplots.AxesSubplot at 0x7ffb6d92ca20>
p_value( data["Conversion_B"], data["Conversion_A"], two_sided=False )t: 3.78736793091929 p: 0.0001818980064144382
(3.78736793091929, 0.0003637960128288764)
Here, p-value < 0.05 show that the convergence rate of website B is better than that of A. Finally, note that this is a one-sided test, so we have not yet tested if the convergence rate of B is worse than that of A. Finally, one of the main downsides of A/B testing for real world data is independence of the datasets as well as existence of multiple variables instead of just 2. Traditional A/B testing extends itself to A/B/C/D.. tests however the problem with these approaches is limited amount of data as well as some variables being more significant while others being weak influencers. We will adress this issue using Bayesian methods.