Light is one of the most amazing phenomena in the Universe. It is pure energy and has zero mass. If you could experience a moment as a photon, you would experience eternity in that moment, for light experiences no time of its own (technically you’d experience nothing as psychological experience is time dependent, but lets keep the poetic tone). It is one of the primordial constituents of the Universe and is considered sacred in all religions, ditto physics. Among other things, a path of light is Brachistochrone.
A Brachistochrone is a path of shortest travel time between any two points (brákhistos:shortest khrónos:time). It is different from shortest path which generally means path with shortest length. For example, one might want to take a longer taxi route between two close points in a city due to traffic. Similarly, if you are trying to reach a friend whose phone is busy, a path with shorter time could be calling their home or someone close to them, etc. as opposed to the shortest path of calling them directly. The Brachistochrone path is defined by constraints in the path, the length of the path being just one of them. Adding more constraints, like time, traffic, etc. means that the overall shortest path has to minimize on additional constraints.
Back to light, in 1905, Einstein had proposed that speed of light is constant. However, his proposal, which became the most important postulate of Special Relativity, ended up implying that the speed of light is the maximum limit to the speed of causality i.e. no two events in causal chain can influence one another faster than light, at least in the non quantum world we live in. We now know that the reason light is brachistochrone (shortest time) in space is because it travels the shortest path in ‘spacetime’, a higher dimensional set of equations that takes into account both the constraints of space and time.
History
The Brachistochrone nature of light was not discovered by Einstein however, nor any physicist but by a mathematician, and a great one, Pierre de Fermat, 250 years earlier, in 16621. This is highly interesting since time has no relevance in mathematics, for it is a distinctly physical phenomenon, but we note that the foundations of physics had yet to be formalized then and just appreciate the caliber of Fermat. In fact, Fermat had nailed the brachistochrone nature of light as the Fermat’s principle states: “light travels between two points along the path that requires the least time, as compared to other nearby paths.”1. Johann Bernoulli, a prominent mathematician in this own right, was aware of Fermat’s principle and having first solved the problem himself in 1696, posed the following to the scientific community of Europe:
The Brachistochrone Problem: To determine the curve jointing two given points, at different distances from the horizontal and not on the same vertical line along which a mobile particle, acted upon by its own weight and starting its motion from the upper point, descents most rapidly to the lower point. (Johann Bernoulli, Acta Eruditorum, June 1696)2
Johann Bernoulli knew that this was a tough problem, even for the giants of his era. In fact, Galileo in 1638 had studied the problem. In his famous work ‘Discourse on two new sciences’, Galileo finds a shorter descent curve compared to a straight line between two points A and B. The path is a circle. Maybe seduced by the perfection of circle, or maybe due to lack to tools necessary to solve this problem (calculus), who knows, Galileo incorrectly concludes that a circular arc is brachistochrone. We today know that the correct curve that solves the problem is a cycloid and not a circle. Ironically, it was Galileo who coined the term ‘cycloid‘ and was the first to make a serious study of the curve3. Anyways, with the help of Fermat, Johann Bernoulli had his ingenious solution. He also knew that he had beat Galileo here. So why not pose the problem to Europe, throw your weight around a little?
Enter the Lion: Issac Newton, 53 years of age, was already considered GOAT by the European scientific community at the time the Brachistochrone problem was posed. However, Johann Bernoulli, along with his buddy Gottfried Leibnitz (another giant, invented integral calculus), wanted to test Newton. Johann Bernoulli had deliberately included these words in this challenge:
“…there are fewer who are likely to solve our excellent problems, aye, fewer even among the very mathematicians who boast that [they]… have wonderfully extended its bounds by means of the golden theorems which (they thought) were known to no one, but which in fact had long previously been published by others..”2
Obviously pointing to Newton-Leibniz controversy over calculus. And here is why Newton is the boss: Newton, who receives the problem from France late in January 1697, comes home around 4 p.m. that day, stays up till 4:00 a.m., solves the problem, mails the solution to Royal society the next day, and in a followup letter mentions “I do not love to be dunned and teased by foreigners about mathematical things.”4. Apparently, Newtons solution was published anonymously. Later when Bernoulli announced the winners of the contest, there was Leibniz, Jacob Bernoulli (the smarter brother, discovered ‘e’), l’Hopital (yep, that guy from 0/0 rule), and the one anonymous winner. Bernoulli recognized this anonymous winner in public,”..tanquam ex ungue leonem..” in Latin, which translates to “I recognize a lion by his claw.”4
Revival
If you are here with me still, I did something Johann Bernoulliesque. I posed the Brachistochrone problem, to myself, but revival had a twist:
The Brachistochrone.ai Problem: To be determined by any silicon based mind, the curve jointing two given points, at different distances from the horizontal and not on the same vertical line along which a mobile particle, acted upon by its own weight and starting its motion from the upper point, descents most rapidly to the lower point.
The reason for this was two fold: First, the problem is of finding an optimal function i.e. a function that minimizes time given dynamics of motion (Newtons laws). We know that Machine Learning is really good at these tasks. In fact, all Machine Learning is is function estimation. There are few really good ones out there: SVMs, GMMs and Neural Networks that have the titles of Universal Function Approximators5. So why not challenge this universality?
The second was an attempt to cast a scientific problem in a language other than calculus. Brachistochrone can be solved easily with Calculus of Variations today. However, just like computing numerical solutions to equations is a huge part of scientific toolbox today, maybe numerical approximations of functions of an unknown relationship and/or dynamics is viable.
Results
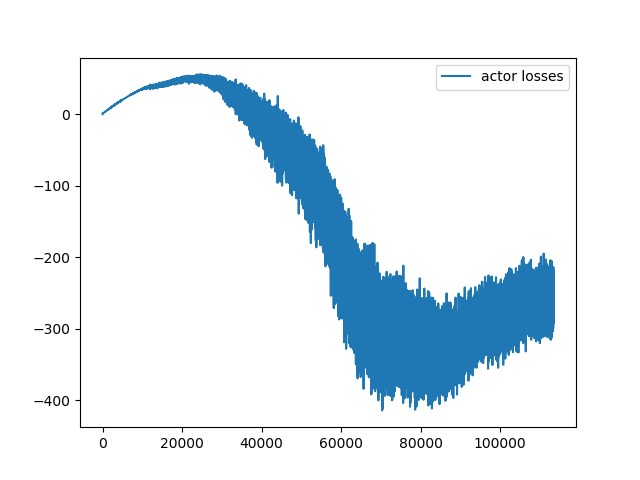
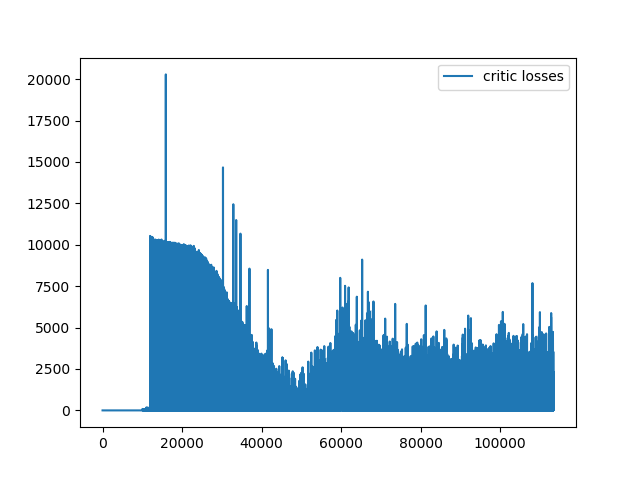
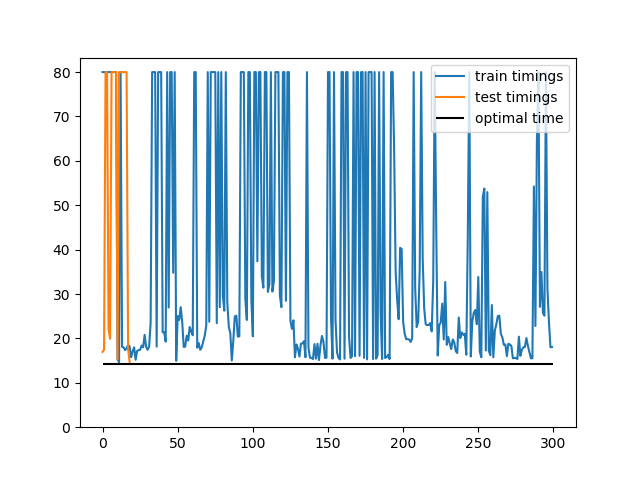
Figures showing the path taken in random, line, circle, cycloid (optimal) paths and by the Reinforcement Learning (AI) agent for three different cases with time step = 0.08. The fourth figure shows case 3 but with time step = 0.5 to enhance random activity.
Summary
So did the AI agent do justice to the history rich Brachistochrone problem? I think we were successful here. Any noisy stochastic system is prone to irregularities but the DDPG managed to give some smooth solutions. Of course they are not the optimal analytical solution of a cycloid generated by a formula in elegance of calculus. But the paths are very close. One exciting next step in AI is to deduce analytic functions from its closest numerical counterparts which is a super hard problem. Meanwhile, an extension to our problem would be to create train and test sets with random starting points and learn the optimal policy to test generalization.
Tying all this back to light, at the time of Fermat, light wasn’t a well known phenomena so the Fermat’s Principle is more of an intelligent conjecture. In his era, light only traveled in straight lines. However, in 1916, Einstein showed that light too yields to gravity and bends its path around massive astronomical bodies. He was able to predict the actual positions of a nearby stars and their deflections from apparent positions precisely using his General theory of Relativity. Today we use the these refraction technique in gravitational lensing which has opened a new doorway to modern astronomy. Note that it was similar refraction that led to Bernoulli’s solution of cycloid. Now that being said, a general brachistochrone problem arises: What is the path that minimizes the proper time of a mobile light particle i.e. a photon between any two points in a spacetime affected only by (strong) gravity? A higher dimensional cycloid?8 The rabbit hole goes way deep..
References
- M. Born and E. Wolf, 1970, Principles of Optics, 4th Ed., Oxford: Pergamon Press.
- P Costabel and J Peiffer (eds.), Bernoulli, Johann I The correspondence of Johann I Bernoulli. Volume 2: The Correspondence with Pierre Varignon: First Part: 1692-1702, The Collected Works of the Mathematicians and Physicists of the Bernoulli Family (Basel, 1988).
- Whitman, E. A. (May 1943), “Some historical notes on the cycloid”, The American Mathematical Monthly, 50 (5): 309–315
- M de Icaza Herrera, Galileo, Bernoulli, Leibniz and Newton around the brachistochronous problem, Rev. Mexicana Fis. 40 (3) (1994), 459-475.
- Balázs Csanád Csáji (2001) Approximation with Artificial Neural Networks; Faculty of Sciences; Eötvös Loránd University, Hungary
- Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra, Continuous control with deep reinforcement learning, CoRR abs/1509.02971 (2015)
- Matthias Plappert et al: “Parameter Space Noise for Exploration”, 2017; arXiv:1706.01905.
- Giannoni, F. et al. A timelike extension of Fermat’s principle in general relativity and applications, P. Calc Var (1998) 6: 263. https://doi.org/10.1007/s005260050091










June 4, 2020
Like!! I blog frequently and I really thank you for your content. The article has truly peaked my interest.
January 9, 2022
hello. topic for me thanks kelly
i found this web and i would to help you with evolution. i am from UAE ;D