Last month I watched Loving Vincent. The movie was a story of Van Gogh post Saint Rémy, in his final year in Auvers-sur-Oise. The story reconstructed the lonely artist’s mental breakdown from the perspectives of people close to him, well at least they are there in his paintings. Aside from reconstruction in a sense of narrative, the movie was also reconstruction in material. The entire movie comprised of animations of reimagined Van Gogh’s paintings. It recreated 94 Van Gogh’s originals while creating about 67K oil paintings around them as animation keyframes. Needless to say it is a huge collaboration of thousands of artists and dedicated hours. You can find details of the behind the scenes here.
This blog is about my experiments with Van Gogh’s paintings and the Neural Style Transer (NST) algorithm. Most of my previous attempts with NST had resulted in mediocre results. The problem is that without a proper metric to judge styles that are intrinsically aesthetic, or without benchmark images to compare against, I didn’t know how and what to improve the algorithm with. Loving Vincent did exactly that, provided me a test bench. In this blog we will use NST to recreate some keyframes of the film. We will compare the results with the movie recreations of Van Gogh paintings.. maybe ponder whether the NST technique could have aided in the production of the movie to save countless hours.. Well, it is said that a pen is mightier than a sword. At times, a brush is mightier than a pen. This blog explores what if, we bring a machine gun to a brush fight.
Theory
This section is my attempt to simplify some concepts that I found confusing with the NST. But I will assume you know what a neural network is and the lingos around it. NST utilizes Convolutional Neural Networks and combines the style of one image with content of the other. Most style transfer mechanisms before neural networks sucked since the problem is highly non-linear in nature ( planning to dedicate another blog on the non-linearity and the mathematics of art). But for NST, the original paper3 does a great job in explaining the architecture and there are a number of tutorials available to help one build it. I played with couple of them but found Keras implementation [here] to be simple and effective to begin with. God is always in the details but to its core, NST is a simple a+b =c algorithm. We use a pre-trained CNN architecture, VGG-19, and combine losses from Content Image (a) and a Style Image (b) that adds up to the final result (c).
a) Content Loss
Let the input image be denoted by vector p. After a feed forward step, an output image x is generated. The pre-trained VGG-19 filters p with encoding on each layer into feature representations Fl that will eventually result in x. Let Pl denote the encoding on the input image p in feature space for that particular convolution layer l. The content loss is the loss measure that minimizes the squared distance between and Pl and Fl. Or,
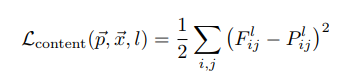
Results
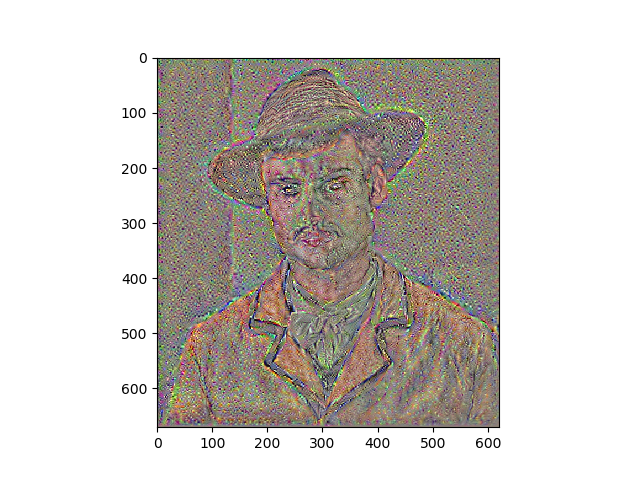
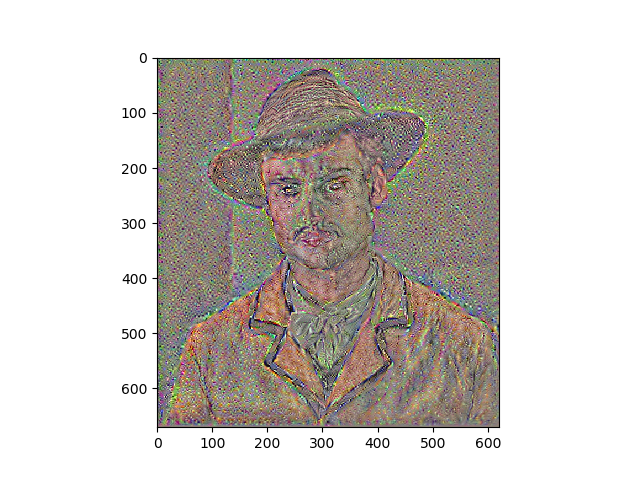
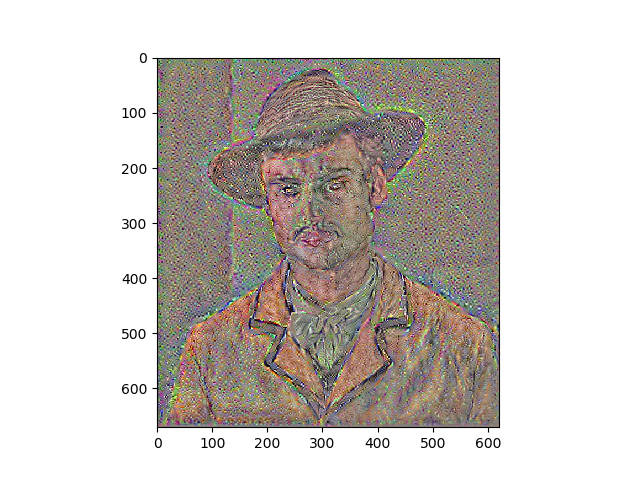
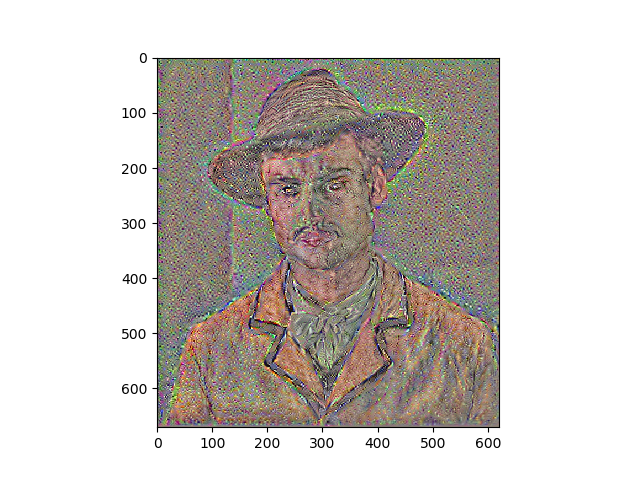
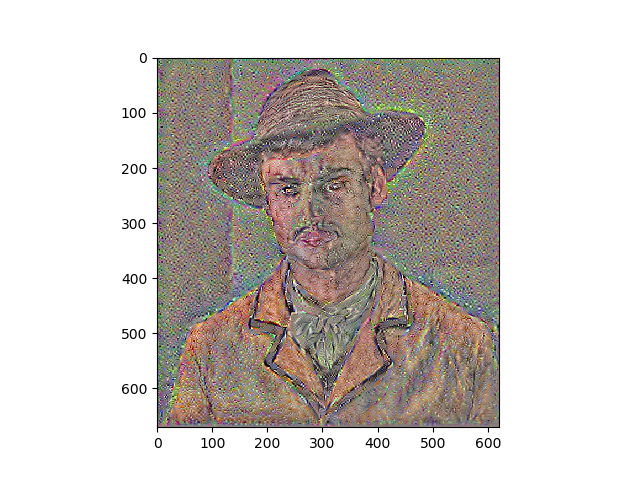
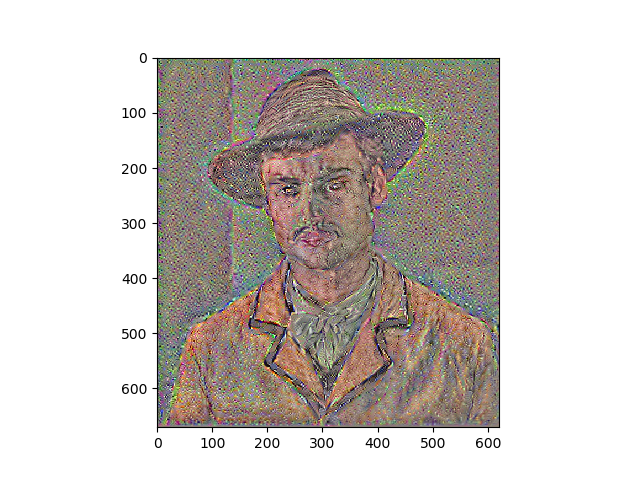
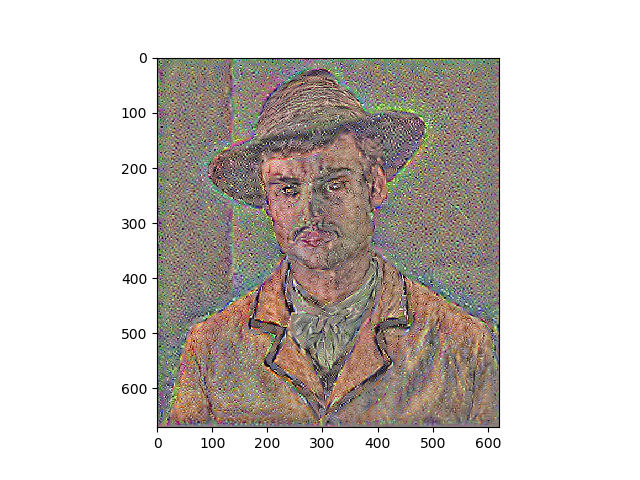
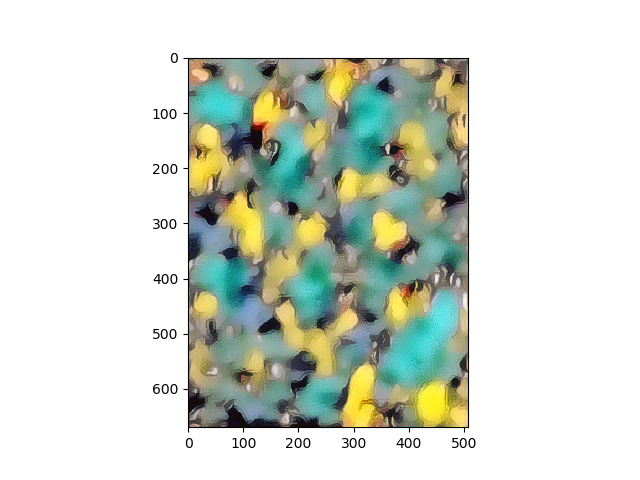
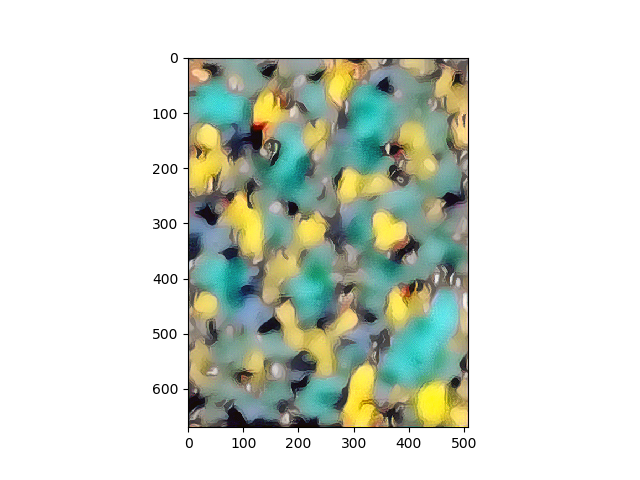
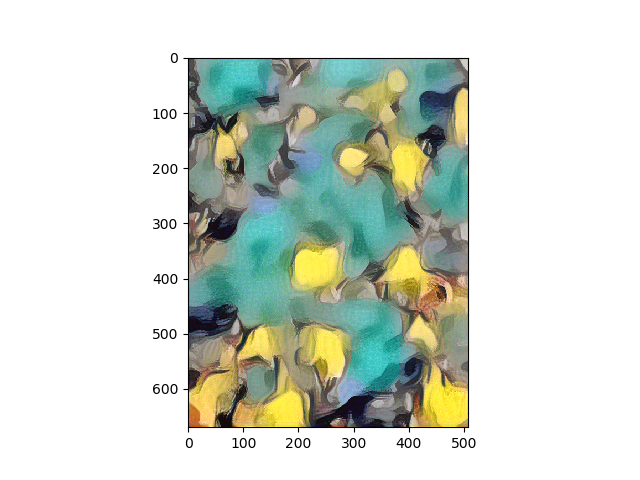
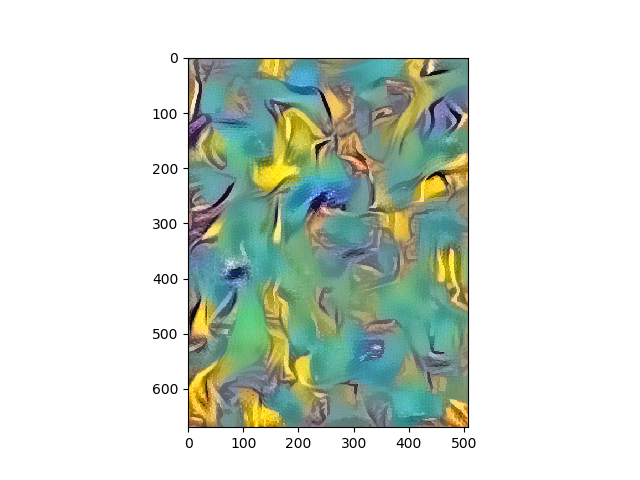
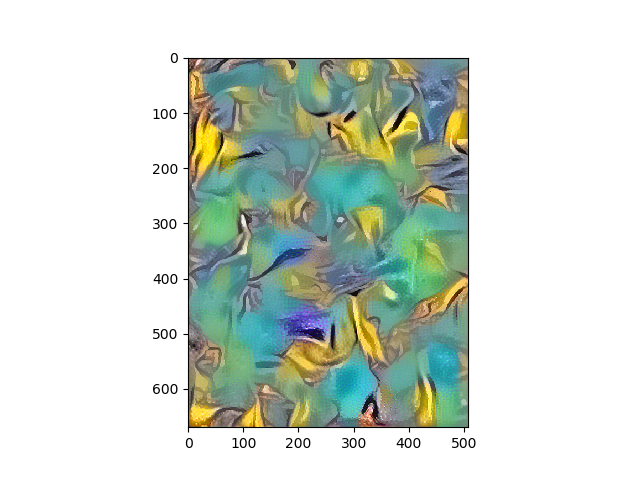
Portraits
Scenes/Landscapes
Summary


So did the Neural Style Transfer do justice to the artist? I think we tried our best. The neural paintings look structurally and aesthetically good after the optimizations, and pretty post impressionist as Van Gogh’s originals. The brush strokes, however, and maybe I need to fine tune the architecture better, I want to leave it up to your judgment. If you did not know about source of the style images, would you have guessed the neural paintings were Van Gogh styled? How far away from Gauguin, Cezanne, Monet, or Degas..
Could NST have helped in creating keyframes in Loving Vincent? At this point, its a yes for me..but the algorithm would quickly break down when subjects from multiple Van Gogh paintings had to interact in a frame. Not to mention, the movie’s soul rests in all the artists’ dedicated work.
The issue of multiple painting subjects is related to what we observed in the Experiment section, that the strength of the algorithm decreased significantly as the style image departed from the content image. It makes sense, as the algorithm is only learning the style of individual painting and not that of an artist, which would be learned from a collection of the artist’s work. I will try to tackle this issue of Artist Style Transfer in my next Fine Arts post. We will bring in some bad boy GANs into the brush fight. Until then, I hope you keep looking up in the starry nights..
References:
- Bethge, Matthias; Ecker, Alexander S.; Gatys, Leon A. (2016). “Image Style Transfer Using Convolutional Neural Networks”. Cv-foundation.org. pp. 2414–2423. Retrieved 13 February 2019.
- Keras Examples Directory, Neural Style Transfer (2018), GitHub repository, https://github.com/keras-team/keras/blob/master/examples/neural_style_transfer.py
- Loving Vincent et al., http://lovingvincent.com




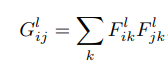
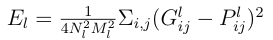
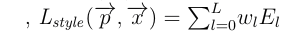



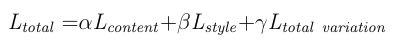















































































November 17, 2019
Really interesting work. The effect is much more pronounced on pictures with higher contrast setting and lesser details. In detailed images (example: garden view), the algorithm seems to skim over a bit and loses its touch. Its fascinating how NST recreated those brush-strokes clearly in some of the paintings. I think you should keep working on it. Loved the concept!