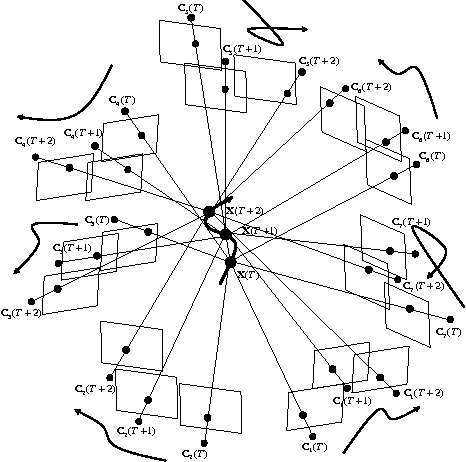
In this project, I extend my multi-view geometry project with bundle adjustment optimization. We are closing in towards multi view sfm reconstuction which is one of the crowning achievements of Computer Vision. In this project we will be adding on to our previous efforts in generating optimized sparse 3D point clouds with the Bundle Adjustment optimization.
Lets begin with importing all of our previous project till now:
import os
import sys
import cv2
import _pickle as pickle
import math
import glob
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinefrom two_view_geometry import two_view_geometry,TriangulatePoints, unitDeterminantCheck,genMatcher, computeDescriptions, plot3D, write_plyLets see what images we have for this reconstruction:
#https://documents.epfl.ch/groups/c/cv/cvlab-unit/www/data/multiview/modelFountain.html
ff, axs = plt.subplots(2,4,figsize=(10,5))
idx=0
for fname in glob.glob('./imgs/fountain/*.png')[:8]:
img = cv2.imread(fname)
plt.subplot(int("24{}".format(idx+1)))
plt.imshow(img.T[[2,1,0]].T)
idx+=1
plt.tight_layout()
plt.show()images_dir = "./imgs/fountain/"
filenames = os.listdir(images_dir)
filenames.sort()ff, axs = plt.subplots(2,4,figsize=(10,10))
idx=0
for fname in glob.glob('./imgs/*.JPEG')[:8]:
gray = cv2.imread(fname)
plt.subplot(int("34{}".format(idx+1)))
plt.imshow(gray)
idx+=1
plt.tight_layout()
plt.show()src_image_path1 = "{}{}".format(images_dir,filenames[0])
src_image_path2 = "{}{}".format(images_dir,filenames[1]calibration_mat_path = "./calib.txt"
distortions_vec_path = None
debug = False
src_image_1 = cv2.imread(src_image_path1, cv2.IMREAD_COLOR)
src_image_2 = cv2.imread(src_image_path2, cv2.IMREAD_COLOR)
K = np.loadtxt(calibration_mat_path)
if distortions_vec_path:
distortions = np.loadtxt(distortions_vec_path)
src_image_1 = cv2.undistort(src_image_1, K, distortions, None, None)
src_image_2 = cv2.undistort(src_image_2, K, distortions, None, None)
src_gray_1 = cv2.cvtColor(src_image_1 , cv2.COLOR_BGR2GRAY)
src_gray_2 = cv2.cvtColor(src_image_2 , cv2.COLOR_BGR2GRAY)
kp1, desc1 = computeDescriptions(src_gray_1, "feats/{}_feats.kp".format(os.path.basename(src_image_path1).split(".")[0]))
kp2, desc2 = computeDescriptions(src_gray_2, "feats/{}_feats.kp".format(os.path.basename(src_image_path2).split(".")[0]))
matcher = genMatcher()
knn_matches = matcher.knnMatch(desc1, desc2, 2)
#-- Filter matches using the Lowe's ratio test
ratio_thresh = 0.8
good = []
pts1 = []
pts2 = []
for m,n in knn_matches:
if m.distance < ratio_thresh * n.distance:
good.append(m)
pts2.append(kp2[m.trainIdx].pt)
pts1.append(kp1[m.queryIdx].pt)
if len(good) <= 10 : #MIN_MATCH_COUNT=10
print( "Not enough matches are found - {}/{}".format(len(good), MIN_MATCH_COUNT) )
pts1 = np.int32(pts1)
pts2 = np.int32(pts2)
#pts1 = np.array(pts1)
#pts2 = np.array(pts2)
F, mask = cv2.findFundamentalMat(pts1, pts2, cv2.FM_RANSAC ) #FM_LMEDS
# We select only inlier points
pts1 = pts1[mask.ravel()==1]
pts2 = pts2[mask.ravel()==1]
Kinv = np.linalg.inv(K)
points_3d, P0, P1 = two_view_geometry( pts1, pts2, F, K )Min Reprojection error: 0.6652368589262047
kp_prev = kp2
desc_prev = desc2
src_image_prev = src_image_2
pts_prev = pts2
points_3d_prev = points_3d
pose_prev = P1
out_pts_3d = points_3d.copy()
out_colors = np.array([ src_image_1[pt[1],pt[0]] for pt in pts1 ])
#for bundle adjustment
out_pts_2d = pts_prev.copy()
rvec,_ = cv2.Rodrigues(P1[:,:3])
out_camera_params = np.hstack([rvec.ravel(), P1[:,3].ravel() ])
view_idx = 0
points_indexes = np.arange(points_3d_prev.shape[0] )
points_indexes_prev = points_indexes.copy()
camera_indexes = np.full( (pts2.shape[0],1), view_idx )
for fname in filenames[2:]:
src_image_path = "{}{}".format(images_dir,fname)
print( src_image_path )
src_image = cv2.imread(src_image_path, cv2.IMREAD_COLOR)
src_gray = cv2.cvtColor(src_image , cv2.COLOR_BGR2GRAY)
kp, desc = computeDescriptions(src_gray, "feats/{}_feats.kp".format(os.path.basename(src_image_path).split(".")[0]))
pts_prev_keys = [ ",".join( list(pt.astype(str) ) ) for pt in pts_prev ]
points_3d_2d = dict( zip( pts_prev_keys, points_indexes_prev ))
knn_matches = matcher.knnMatch(desc_prev, desc, 2)
#-- Filter matches using the Lowe's ratio test
ratio_thresh = 0.8
good = []
pts_a = []
pts_b = []
for m,n in knn_matches:
if m.distance < ratio_thresh * n.distance:
good.append(m)
pts_b.append(kp[m.trainIdx].pt)
pts_a.append(kp_prev[m.queryIdx].pt)
pts_a = np.array(pts_a)
pts_b = np.array(pts_b)
# Using Epiplolar Constraint to filter only inlier points
F, mask = cv2.findFundamentalMat(pts_a, pts_b, cv2.FM_RANSAC )
pts_a = pts_a[mask.ravel()==1]
pts_b = pts_b[mask.ravel()==1]
pts_a = np.int32(pts_a)
#Select 3d points that were seen in previous image view
points_3d_cur_index = np.array([ points_3d_2d.get( ",".join( list(pt.astype(str)) ) ) for pt in pts_a ])
pts_mask = np.array([ True if idx != None else False for idx in points_3d_cur_index ])
points_3d_cur = np.array([ out_pts_3d[idx] if idx != None else [0,0,0,1] for idx in points_3d_cur_index])
retval, rvecs, tvecs, inliers = cv2.solvePnPRansac(points_3d_cur[ pts_mask ][:,:-1], pts_b[pts_mask] , K, None)
pts_b = np.int32(pts_b)
R_mat, _ = cv2.Rodrigues(rvecs)
if not unitDeterminantCheck(R_mat):
print("Not a rotation matrix")
break
#triangulate new 3d points
pose = np.column_stack( [ R_mat, tvecs ] )
points_3d_cur2, err = TriangulatePoints( pts_a[ ~pts_mask ], pts_b[ ~pts_mask ], K, Kinv, pose_prev, pose )
print("Reprojection error:", err)
points_3d_cur[~pts_mask] = points_3d_cur2
#for bundle adjustment
out_camera_params = np.vstack( [ out_camera_params, np.hstack([rvecs.ravel(), tvecs.ravel() ]) ])
out_pts_2d = np.concatenate( [ out_pts_2d, pts_b ], axis=0)
#points_indexes_cur = np.concatenate([ points_3d_cur_index[ pts_mask ], out_pts_3d.shape[0] + np.arange(points_3d_cur2.shape[0]) ])
points_indexes_cur = points_3d_cur_index.copy()
points_indexes_cur[ ~pts_mask ] = out_pts_3d.shape[0] + np.arange(points_3d_cur2.shape[0])
points_indexes = np.concatenate( [ points_indexes, points_indexes_cur ], axis=0)
out_pts_3d = np.concatenate([out_pts_3d, points_3d_cur2 ], axis=0)
#print(out_pts_3d.shape, points_3d_cur.shape)
out_colors_cur = np.array([ src_image_prev[pt[1],pt[0]] for pt in pts_a[ ~pts_mask ] ])
out_colors = np.concatenate([out_colors, out_colors_cur],axis=0)
camera_indexes = np.concatenate( [ camera_indexes, np.full( (pts_b.shape[0],1), view_idx+1 ) ] )
kp_prev = kp
desc_prev = desc
src_image_prev = src_image
#pts_prev = np.concatenate( [ pts_b[pts_mask],pts_b[~pts_mask] ],axis=0 )
pts_prev = pts_b
#points_3d_prev = points_3d_cur
points_indexes_prev = points_indexes_cur
#points_3d_prev = np.concatenate( [ points_3d_cur[pts_mask],points_3d_cur[~pts_mask] ],axis=0 )
pose_prev = pose
view_idx += 1
./imgs/fountain/0002.png
Reprojection error: 0.4153691027131726
./imgs/fountain/0003.png
Reprojection error: 0.7298518688105945
./imgs/fountain/0004.png
Reprojection error: 0.8731119082957116
./imgs/fountain/0005.png
Reprojection error: 0.6056678112261642
./imgs/fountain/0006.png
Reprojection error: 0.44378746796326785
./imgs/fountain/0007.png
Reprojection error: 0.5167973110556678
./imgs/fountain/0008.png
Reprojection error: 0.4270353889380259
./imgs/fountain/0009.png
Reprojection error: 0.720796500553381
./imgs/fountain/0010.png
Reprojection error: 0.5737068350362619
Ok, lets observe the reprojection error of each 3D point to whichever view camera it was viewed upon. According to our scheme we only favored the first 3D point triangulated from the first 2 views.
"""
https://scipy-cookbook.readthedocs.io/items/bundle_adjustment.html
"""
def rotate(points, rot_vecs):
"""Rotate points by given rotation vectors.
Rodrigues' rotation formula is used.
"""
theta = np.linalg.norm(rot_vecs, axis=1)[:, np.newaxis]
with np.errstate(invalid='ignore'):
v = rot_vecs / theta
v = np.nan_to_num(v)
dot = np.sum(points * v, axis=1)[:, np.newaxis]
cos_theta = np.cos(theta)
sin_theta = np.sin(theta)
return cos_theta * points + sin_theta * np.cross(v, points) + dot * (1 - cos_theta) * v
def project(points, camera_params, camera_intrinsics):
"""Convert 3-D points to 2-D by projecting onto images."""
points_proj = rotate(points, camera_params[:, :3])
points_proj += camera_params[:, 3:6]
fx = camera_intrinsics[0, 0]
fy = camera_intrinsics[1, 1]
cx = camera_intrinsics[0, 2]
cy = camera_intrinsics[1, 2]
points_proj = np.array([ points_proj[:,0]*fx + cx*points_proj[:,2], points_proj[:,1]*fy + cy*points_proj[:,2], points_proj[:,2] ]).T
points_proj = points_proj[:, :2] / points_proj[:, 2, np.newaxis]
return points_proj
def fun(params, n_cameras, n_points, camera_indices, point_indices, points_2d, K):
"""Compute residuals.
`params` contains camera parameters and 3-D coordinates.
"""
camera_params = params[:n_cameras * 6].reshape((n_cameras, 6))
points_3d = params[n_cameras * 6:].reshape((n_points, 3))
points_proj = project(points_3d[point_indices], camera_params[camera_indices], K )
return np.abs(points_proj - points_2d).ravel()n_cameras = view_idx+1
n_points = out_pts_3d.shape[0]
camera_indices = camera_indexes.ravel()
point_indices = points_indexes.astype(np.int32)
x0 = np.hstack((out_camera_params.ravel(), out_pts_3d[:,:3].ravel()))
f0 = fun(x0, n_cameras, n_points, camera_indices, point_indices, out_pts_2d, K)
plt.plot(f0)We note existence of outlier 3D points that takes the reprojection error to inf. A naive Bundle adjustment mechanism would be hijacked by these outliers and the algorithm will try its best to minimize these anomalies. Try it out if you dont believe me. Anyways, the best thing to do is to remove these 3d and 2d points from out view since we have enough of these to go around.
def isOutlier(f, res=3):
#an outlier is any point that deivates from 3sdtev from mean
mu = f.mean()
dev = f0.std()
return ( f > (mu + res * dev) ) | ( f < (mu - res * dev) )f0_2d = f0.reshape(-1,2)
f0_2d_norm = np.array([ np.linalg.norm(pt) for pt in f0_2d ])
plt.plot(f0_2d_norm)
outlier = isOutlier(f0_2d_norm)Lets remove the outliers from out 3d-2d correspondences
n_cameras = view_idx+1
n_points = out_pts_3d.shape[0]
camera_indices = camera_indexes[~outlier].ravel()
point_indices = points_indexes[~outlier].astype(np.int32)
x1 = np.hstack((out_camera_params.ravel(), out_pts_3d[:,:3].ravel()))
f1 = fun(x1, n_cameras, n_points, camera_indices, point_indices.copy(), out_pts_2d[~outlier], K)
plt.plot(f1)Ok, looks like we can deal with this range of errors. Lets run the Bundle Adjustment mechanism on it then.
from scipy.sparse import lil_matrix#we are only trying to optimize camera extrinsics and the 3d points
def bundle_adjustment_sparsity(n_cameras, n_points, camera_indices, point_indices):
m = camera_indices.size * 2
n = n_cameras * 6 + n_points * 3
A = lil_matrix((m, n), dtype=int)
i = np.arange(camera_indices.size)
for s in range(6):
A[2 * i, camera_indices * 6 + s] = 1
A[2 * i + 1, camera_indices * 6 + s] = 1
for s in range(3):
A[2 * i, n_cameras * 6 + point_indices * 3 + s] = 1
A[2 * i + 1, n_cameras * 6 + point_indices * 3 + s] = 1
return AA = bundle_adjustment_sparsity(n_cameras, n_points, camera_indices, point_indices)import time
from scipy.optimize import least_squarest0 = time.time()
res = least_squares(fun, x1, jac_sparsity=A, verbose=2, x_scale='jac', ftol=1e-8, method='trf',
args=(n_cameras, n_points, camera_indices, point_indices, out_pts_2d[~outlier], K))
t1 = time.time() Iteration Total nfev Cost Cost reduction Step norm Optimality
0 1 3.1321e+06 9.84e+06
1 4 1.7900e+06 1.34e+06 3.79e+00 3.54e+06
2 5 9.5232e+05 8.38e+05 7.34e+00 9.73e+05
3 6 6.1830e+05 3.34e+05 2.88e+01 1.72e+06
4 7 5.2911e+05 8.92e+04 1.05e+02 1.53e+06
5 8 5.2053e+05 8.58e+03 2.31e+02 6.32e+05
6 9 5.1460e+05 5.94e+03 4.65e+02 4.38e+05
7 10 5.1357e+05 1.02e+03 1.34e+01 3.04e+04
8 11 5.1353e+05 4.09e+01 3.93e-01 2.53e+03
9 14 5.1353e+05 1.09e-01 6.67e-02 3.42e+03
10 15 5.1353e+05 9.85e-02 3.14e-02 2.20e+03
11 16 5.1353e+05 2.88e-02 6.77e-02 1.21e+03
12 17 5.1353e+05 3.69e-03 6.88e-02 3.42e+03
13 18 5.1353e+05 5.19e-02 3.51e-03 8.18e+02
14 19 5.1353e+05 5.59e-03 1.75e-02 8.62e+02
15 20 5.1353e+05 1.10e-02 1.73e-02 8.68e+02
16 21 5.1353e+05 1.04e-02 3.51e-02 8.59e+02
17 22 5.1353e+05 2.37e-02 3.51e-02 7.93e+02
18 23 5.1353e+05 5.55e-03 7.08e-02 5.12e+03
19 24 5.1353e+05 3.66e-02 4.40e-03 9.51e+02
20 25 5.1353e+05 6.38e-03 1.79e-02 8.99e+02
21 26 5.1353e+05 9.60e-03 1.78e-02 7.98e+02
22 27 5.1353e+05 1.24e-02 3.58e-02 8.17e+02
23 28 5.1353e+05 1.92e-02 3.59e-02 6.50e+02
24 29 5.1353e+05 1.35e-02 7.22e-02 1.46e+03
25 30 5.1353e+05 3.01e-02 7.23e-02 5.48e+03
26 31 5.1353e+05 4.54e-02 7.21e-02 2.72e+03
27 32 5.1353e+05 2.83e-02 1.46e-01 2.59e+03
28 33 5.1353e+05 5.68e-02 1.02e-01 4.55e+03
29 34 5.1353e+05 6.17e-02 9.63e-02 3.28e+03
30 35 5.1353e+05 6.05e-02 1.44e-01 2.56e+03
31 36 5.1353e+05 3.75e-02 8.65e-02 1.88e+03
32 37 5.1353e+05 3.50e-02 7.56e-02 2.30e+03
33 38 5.1353e+05 2.96e-02 7.46e-02 2.13e+03
34 39 5.1353e+05 2.98e-02 5.98e-02 1.66e+03
35 40 5.1353e+05 2.06e-02 8.25e-02 2.01e+03
36 41 5.1353e+05 3.58e-02 5.34e-02 1.99e+03
37 42 5.1353e+05 2.63e-02 1.02e-01 3.14e+03
38 43 5.1353e+05 3.95e-02 4.84e-02 1.62e+03
39 44 5.1353e+05 1.19e-02 1.17e-01 2.70e+03
40 45 5.1353e+05 5.65e-02 4.76e-02 1.68e+03
41 46 5.1353e+05 1.66e-02 1.34e-01 3.17e+03
42 47 5.1353e+05 5.64e-02 4.15e-02 1.46e+03
43 49 5.1353e+05 1.82e-02 4.22e-02 4.01e+02
44 51 5.1353e+05 8.70e-03 2.16e-02 5.28e+02
45 52 5.1353e+05 1.58e-02 4.32e-02 1.54e+03
46 53 5.1353e+05 1.38e-02 8.63e-02 1.49e+03
47 55 5.1353e+05 2.94e-02 2.11e-02 2.00e+03
48 56 5.1353e+05 2.20e-02 4.30e-02 5.46e+02
49 57 5.1353e+05 7.02e-03 8.63e-02 2.03e+03
50 58 5.1353e+05 3.26e-02 6.10e-03 7.29e+02
51 59 5.1353e+05 8.63e-03 2.15e-02 6.07e+02
52 60 5.1353e+05 1.24e-02 4.31e-02 1.23e+03
53 61 5.1353e+05 2.03e-02 4.30e-02 3.39e+02
54 63 5.1353e+05 9.92e-03 2.15e-02 6.18e+02
55 64 5.1353e+05 1.37e-02 4.30e-02 1.56e+03
56 65 5.1353e+05 2.02e-02 4.29e-02 9.64e+02
57 67 5.1353e+05 9.28e-03 2.15e-02 9.17e+02
58 68 5.1353e+05 1.23e-02 2.14e-02 3.29e+02
59 70 5.1353e+05 4.05e-03 1.08e-02 4.44e+02
`ftol` termination condition is satisfied.
Function evaluations 70, initial cost 3.1321e+06, final cost 5.1353e+05, first-order optimality 4.44e+02.
camera_params = res.x[:n_cameras * 6].reshape((n_cameras, 6))
points_3d = res.x[n_cameras * 6:].reshape((n_points, 3))plt.plot(res.fun)Compared to the previous residuals, the max error is now under 370 vs around 500 without Bundle Adjustment. The errors towards the higher view Indexes (newer 3d Points) which seemed distrubute around 60 pixel values pre optimzation are now significantly lower with Bundle Adjustment (i.e. in range < 10 pixels).
write_ply("./out1.ply", points_3d, out_colors.T[[2,1,0]].T)References
Multiple View Geometry in Computer Vision (second edition), R.I. Hartley and A. Zisserman, Cambridge University Press, ISBN 0-521-54051-8